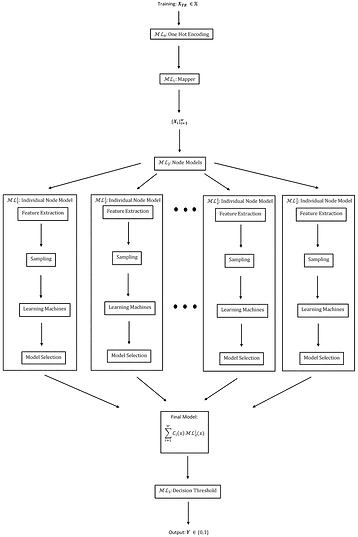
Machine Learning Morphisms

Machine Learning Morphisms (MLM) are a mathematical framework to describe Machine Learning Applications. They are designed to encode as many operations as possible, from preprocessing to feature engineering to model training.

MLM's can mathematically be described as a 5-tuple:

Input probability space
Output probability space
Learning morphism
Prior distribution on parameters
Empirical risk function

The parameters are learned by optimizing the empirical risk function over a set of data.

The key idea with MLM's is the idea of composition which allows us to chain together operations and represent a workflow as a single mathematical object. This allows for potential joint optimization and modular design.

As an application, I built a machine learning model to predict 30-Day hospital readmissions. This model incorporates the TDA Mapper algorithm in a novel way to create an ensemble model that improves over the current tools used by Barnes Jewish Hospital.

A full description of MLM's can be found here.

A set of properties and operations used to design MLM's:

Asymptotic Equality: Concept of equality of two workflows based on the expected risk.
Structural Composition: Joint Optimization of Parameters.
Output Composition: Sequential Optimization of Parameters.
Workflow: Sequence of compositions.
Separability: Parameters can be learned by solving smaller dimensional Problems.

Publications:

[1]: E. Cawi, P. S. La Rosa, and A. Nehorai, "Designing machine learning workflows with an application to topological data analysis," PLOS ONE, Vol. 14, No. 12, pp. 1-26, Dec. 2019.

[2]: A. C. Tukpah, E. Cawi (Co-First), L. Wolf, A. Nehorai; L. Cummings-Vaughn (2020), "Development of an Institution Specific Readmission Risk PredictionModel for Real-Time Prediction and Patient-Centered Interventions",in revision for Journal of General Internal Medicine, 2020.

[3]: E. Cawi, P.S. La Rosa, and A. Nehorai, "Conditions for Separability of Machine Learning Workflows", submitted, Journal of Artficial Intelligence Research

[4]: E. Cawi, P.S. La rosa, and A. Nehorai, "Covariance Bounds for Machine Learning Workflows" (Working title), in preparation.